ZWICHRZENIE BELEK
W podejściu teoretycznym i numerycznym. Artykuł dotyczy niestateczności elementów belkowych przy zginaniu. Podjęto w nim próbę inżynierskiego objaśnienia zjawiska zwichrzenia oraz sposobu obliczania momentu krytycznego przy użyciu powszechnie znanych wzorów analitycznych oraz – jako alternatywę – programów obsługujących metodę elementów skończonych.
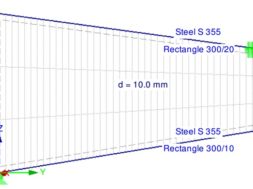
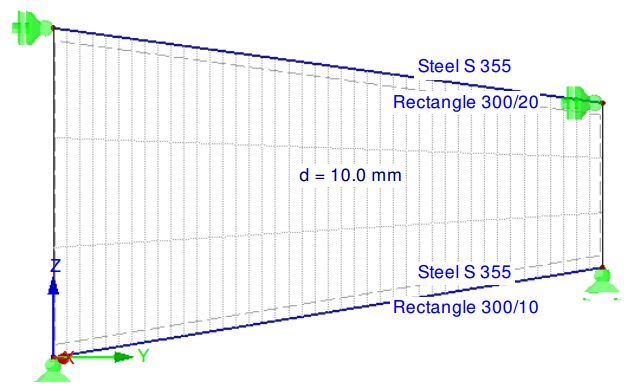
W codziennej praktyce inżynierskiej często zachodzi potrzeba wyznaczenia momentu krytycznego dla elementów prętowych. Wzory uzyskane na drodze ścisłych rozważań teoretycznych sprawdzają się dla prostych przypadków (np. belka swobodnie podparta), lecz dla elementów o bardziej skomplikowanych warunkach podparcia i nietypowych przebiegach momentów gnących standardowe wzory mogą okazać się niewystarczające, a wyniki z nich uzyskane – niemiarodajne. Wychodząc naprzeciw tym wymaganiom, autorzy niniejszego artykułu prezentują prostą metodę pozwalającą uzyskiwać zadowalające wyniki.
Artykuł jest skierowany do osób mających podstawową wiedzę z wytrzymałości materiałów i został napisany w celu usystematyzowania ogólnej wiedzy o zjawisku zwichrzenia od strony teoretycznej i numerycznej.
Teoria prętów cienkościennych
Z pojęciem zwichrzenia belek o przekrojach cienkościennych otwartych nierozerwalnie wiąże się teoria profili cienkościennych (teoria Własowa). Na jej gruncie łatwo daje się wytłumaczyć zjawisko niestateczności płaskiej postaci zginania. W celu uproszczenia zagadnienia poniższe rozważania oparto na przykładzie belki o przekroju dwuteowym bisymetrycznym. Teoria Własowa wychodzi poza klasyczną teorię skręcania prętów zaproponowaną przez de Saint-Venanta. Okazuje się bowiem, że o ile dla prętów litych bądź cienkościennych o przekrojach zamkniętych zasada de Saint-Venanta jest spełniona, tak zastosowanie jej w przypadku prętów cienkościennych o przekroju otwartym byłoby sporym nadużyciem i w obliczeniach inżynierskich jest niemiarodajne.